Guía programación lógica

Los siguientes ejercicios deben ser pensados dentro del paradigma lógico. Pueden ser resueltos utilizando otros paradigmas pero el objetivo es el de lograr resolverlos utilizándolo, específicamente utilizando el lenguaje Prolog. Para resolverlos se deben utilizar los conceptos y las herramientas vistas en clase, aunque puede ser necesario para resolverlos investigar otras herramientas por propia cuenta.

Ejercicios básicos

  1. (★) Sea la siguiente base de conocimiento:

    cursa(emiliano, paradigmas).
cursa(camila, algo2).
cursa(ramiro, tda).
cursa(micaela, paradigmas).

dicta(martin, algo2).
dicta(martin, tda).
dicta(mati, paradigmas).
dicta(fede, paradigmas).
dicta(nacho, paradigmas).

profesor(X,Y) :- dicta(X, Z), cursa(Y, Z).

    Cómo responde Prolog a las siguientes consultas?

    cursa(emiliano, algo2).
cursa(emiliano, paradigmas).
cursa(emiliano, algo3).
dicta(mati, paradigmas).
dicta(fede, X).
dicta(X, paradigmas).
profesor(martin, emiliano).
profesor(nacho, X)
  2. (★★) Partiendo de la relacion progenitor(a, b) que representan que a es padre o madre de b, y la siguiente base de conocimiento: 
       progenitor(a,b).  % 1
   progenitor(a,c).  % 2
   progenitor(b,d).  % 3
   progenitor(b,e).  % 4
   progenitor(c,f).  % 5

    Definir los siguientes predicados:

    • hermano(X, Y) que se cumple si X e Y son hermanos
    • primo(X, Y) que se cumple si X e Y son primos
    • nieto(X, Y) que se cumple si X es nieto de Y
    • descendiente(X, Y) que se cumple si X es descendiente de Y

    Realizar las consultas correspondientes para determinar:

    • Todos los hermanos
    • Todos los primos de e
    • Todos los nietos de a
    • Todos los descendientes de b

  3. (★★★) Sean las palabras en italiano

    astante , astoria , baratto , cobalto , pistola , statale .

    Se desea aplicarlas en el siguiente crucigrama:

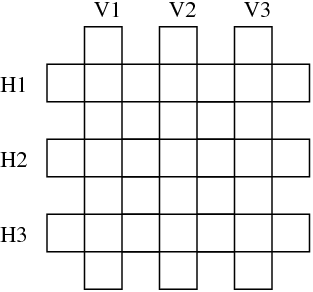
    Escribir una base de datos y una consulta que encuentre una solución al problema.

  4. (★★★) Dadas la siguiente base de conocimiento:

    byCar(auckland,hamilton).
byCar(hamilton,raglan).
byCar(valmont,saarbruecken).
byCar(valmont,metz).

byTrain(metz,frankfurt).
byTrain(saarbruecken,frankfurt).
byTrain(metz,paris).
byTrain(saarbruecken,paris).

byPlane(frankfurt,bangkok).
byPlane(frankfurt,singapore).
byPlane(paris,losAngeles).
byPlane(bangkok,auckland).
byPlane(singapore,auckland).
byPlane(losAngeles,auckland).

    Escribir un predicado travel que permita averiguar si es posible o no viajar de una ciudad a otra, ya sea en uno o más tramos.

Ejercicios arbol de ejecución

  1. Dada la siguiente base de conocimiento y predicados:

    apruebaParcial(ricardo).
apruebaParcial(juana).
profesorAmigo(ricardo, profesor1).
profesorAmigo(ricardo, profesor2).
profesorAmigo(santiago, profesor2).
esProfesor(profesor1).

apruebaCursada(X) :- apruebaParcial(X), profesorAmigo(X, Y),esProfesor(Y).

    Escribir el arbol de ejecución de Prolog la pregunta apruebaCursada(ricardo).

  2. Dada la siguiente base de conocimiento y predicados:

    apruebaParcial(juana).
apruebaParcial(ricardo).
profesorAmigo(ricardo, profesor2).
profesorAmigo(ricardo, profesor1).
profesorAmigo(santiago, profesor1).
esProfesor(profesor1).

apruebaCursada(X) :- apruebaParcial(X), profesorAmigo(X, Y),esProfesor(Y).

    Escribir el arbol de ejecución de Prolog la pregunta apruebaCursada(ricardo)

Ejercicios aritmetica

  1. (★) Definir la relación máximo(X,Y,Z) que se verifique si Z es el máximo de X e Y.

  2. (★★) Definir la relación fatorial(X,Y) que se verifique si Y es el factorial de X.

  3. (★★★) La sucesión de Fibonacci es 0,1,1,2,3,5,8,13,21,. . . en la que cada término, salvo los dos primeros, es la suma de los dos anteriores. Definir la relación fibonai(N,X) que se verifique si X es el N–ésimo término de la sucesión de Fibonacci.

Ejercicios listas

  1. (★) Definir la relación cons(X,L1,L2) que se verifique si L2 es la lista obtenida añadiéndole X a L1 como primer elemento.

  2. (★) Un palíndromo es una palabra que se lee igual en los dos sentidos, por ejemplo “oso”. Definir la relación palíndromo(L) que se verifique si la lista L es un palíndromo.

  3. (★) Definir la relación todos_iguales(L) que se verifique si todos los elementos de la lista L son iguales entre sí.

  4. (★★) Definir la relación max_lista(L,X) que se verifique si X es el máximo de la lista de números L.

  5. (★★★) Definir la relación elemento_en(K,L,X) que se verifique si X es el K–ésimo elemento de la lista L (se empieza a numerar en 1).

Ejercicios avanzados

  1. (★★★) Se tiene el siguiente mapa compuesto por 5 regiones (A, B, C, D y E), se desea identificar si es posible colorear el mapa usando solo 4 colores, de forma tal que ninguna region sea adyacente a otra región con el mismo color.

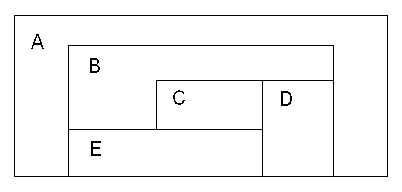
  2. (★★★★) Hay 4 estudiantes: Carrie, Erma, Ora und Tracy. Todos ellos estudian una carrera de grado y están becados (todos tienen becas distintas y estudian distintas carreras). El objetivo es identificar cual es la beca que recibe cada estudiante y cual es la carrera de grado que estudia a partir de las siguientes pistas:

    • Las becas disponibles son: 25000, 30000, 35000 and 40000 USD.
    • Las carreras disponibles son: Astronomia, Ingles, Filosofía y Física.
    • El estudiante que estudia Astronomía tiene una beca menor que la de Ora.
    • Ora estudia Ingles o Filosofía
    • El estudiante que estudia Física, tiene una beca 5000 USD mayor que la beca de Carrie.
    • Erna tiene una beca 10000 USD mayor que la beca de Carrie.
    • Tracy tiene una beca mayor que la que tiene el que estudia Ingles.